Context-free Languages

A good starting example for what is so-called “context-free grammars” is to look at the English language we’re using everyday. I would present a very simple way of describe our language. Each sentence in English, to put simply, is made of a noun phrase and a verb phrase. A noun phrase may contain another noun, a verb phrase may contain a preposition phrase or another noun. You see, these terms are defined recursively, and it is very difficult or impossible to describe such a language using finite automata or regular expression. Context-free grammar (CFG) is a powerful tool to deal with languages with recursive structure. Using the example above, one can write a CFG like this (taken directly from [1]):

Sentence \(\rightarrow\) Noun-phrase Verb-phrase
Noun-phrase \(\rightarrow\) Complex-noun or Complex-noun Preposition-phrase
Verb-phrase \(\rightarrow\) Complex-verb or Complex-verb Preposition-phrase
Preposition-phrase \(\rightarrow\) Preposition Complex-noun
Complex-noun \(\rightarrow\) Article Noun
Complex-verb \(\rightarrow\) Verb or Verb Noun-phrase
Article \(\rightarrow\) a or the
Noun \(\rightarrow\) boy or girl or knife
Verb \(\rightarrow\) touches or cuts or sees
Preposition \(\rightarrow\) with

Now, if I tell you to construct a sentence from this grammar, you may want to derive it as follows (whenever you have several options to derive a variable, e.g. Noun-phrase, Verb-phrase, etc., you are free to choose any option):

1. Sentence \(\Rightarrow\) Noun-phrase Verb-phrase
2.  \(\Rightarrow\) Complex-noun Complex-verb Preposition-phrase
3.  \(\Rightarrow\) Article Noun Verb Preposition Complex-noun
4.  \(\Rightarrow\) Article Noun Verb Preposition Article Noun
5.  \(\Rightarrow\) the boy cuts with a knife

You can come up with something like the boy touches with the girl, which completely sounds nonsense, but does not violate any substitution rules (there are 18 rules, written in 10 lines above) at all. Some other sentences are:

• the boy touches the girl
• the boy cuts the girl with a knife
• the knife cuts the boy

In this post we’re going to discuss several concepts surrounding context-free languages.

Context-free grammar

Consider a simpler example, a grammar G:

On the left hand side of the arrows, A and B are called variables. The strings on the other side consist of variables and terminals. Terminals are symbols taken from the alphabet, and sometimes can be confused with variables, so we usually use capital letters for variables and lowercase / special / number characters for terminals. Each line depicts a substitution rule, aka production. The variable of the first line (i.e. on the left of the arrow) is usually the start variable, unless specified otherwise.

You can generate a string from the grammar by following simple routine as follows:

1. Write the start variable
2. Replace a variable in our current string with a string using any one of the grammar rules of that variable
3. Repeat step 2 until there is no variable left in the string

Example:

A \(\Rightarrow\) 0A1 \(\Rightarrow\) 00A11 \(\Rightarrow\) 000A111 \(\Rightarrow\) 0001B0111 \(\Rightarrow\) 00011B00111 \(\Rightarrow\) 0001100111

The process above is called a derivation, we can write \(A\xRightarrow{*}0001100111\), and say A derives 0001100111. At each step, e.g. \(A\Rightarrow 0A1\), we can say A yields 0A1.

The grammar above can be short-written as (the vertical bar means or):

In general, the language of this grammar is \(\{0^n1^m0^m1^n\vert\ n\geq 0, m\geq 1\}\), denoted as L(G). It is called a context-free language if there is some CGF generating it.

Definition: Context-free Grammar. A context-free grammar (CFG) is a tuple \((V, \Sigma, R, S)\), where

• V is a finite set of variables
•  \(\Sigma\) is a finite set of terminals, disjoint from V
• R is a finite set of rules
•  \(S\in V\) is the start variable

From DFA to CFG

If we have a regular language and a DFA that recognizes it, we can construct a CFG much more easily. Suppose the DFA has n states, we shall create n respected variables. For any transition \(\delta(q_i, a) = q_j\), we add a rule \(R_i\rightarrow aR_j\). For any accepting state \(q_i\), add a rule \(R_i\rightarrow \epsilon\), and finally make \(R_0\) the start variable (with the assumption that \(q_0\) is the start state).

Union of two CFLs

Suppose you have two CFL whose CFG’s start variables are \(S_1\) and \(S_2\). The union of these two languages is also a CFL, by combining two grammars together and an extra rule \(S\rightarrow S_1\ \vert\ S_2\), where \(S\) is the start variable of the union.

Ambiguity

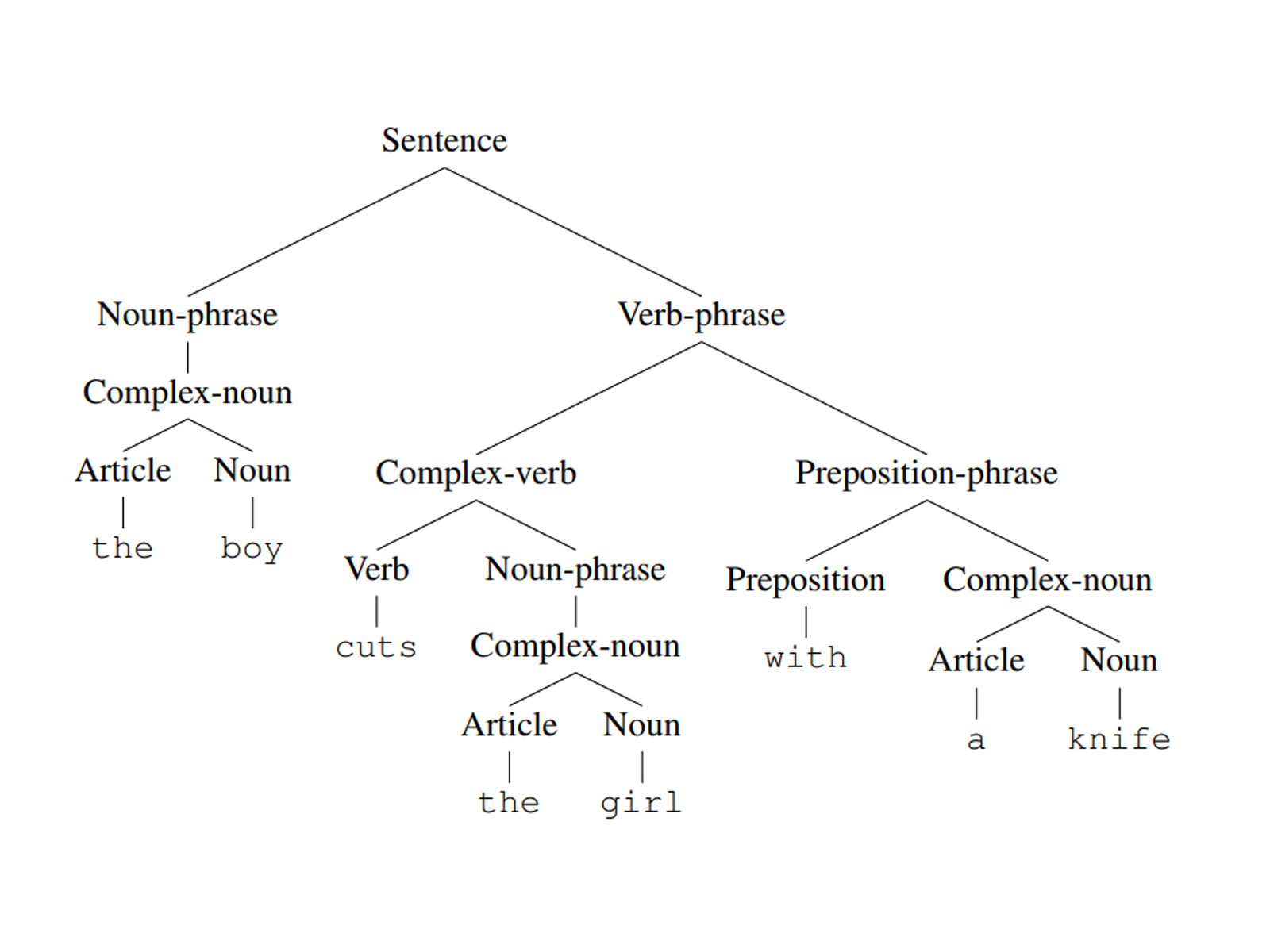
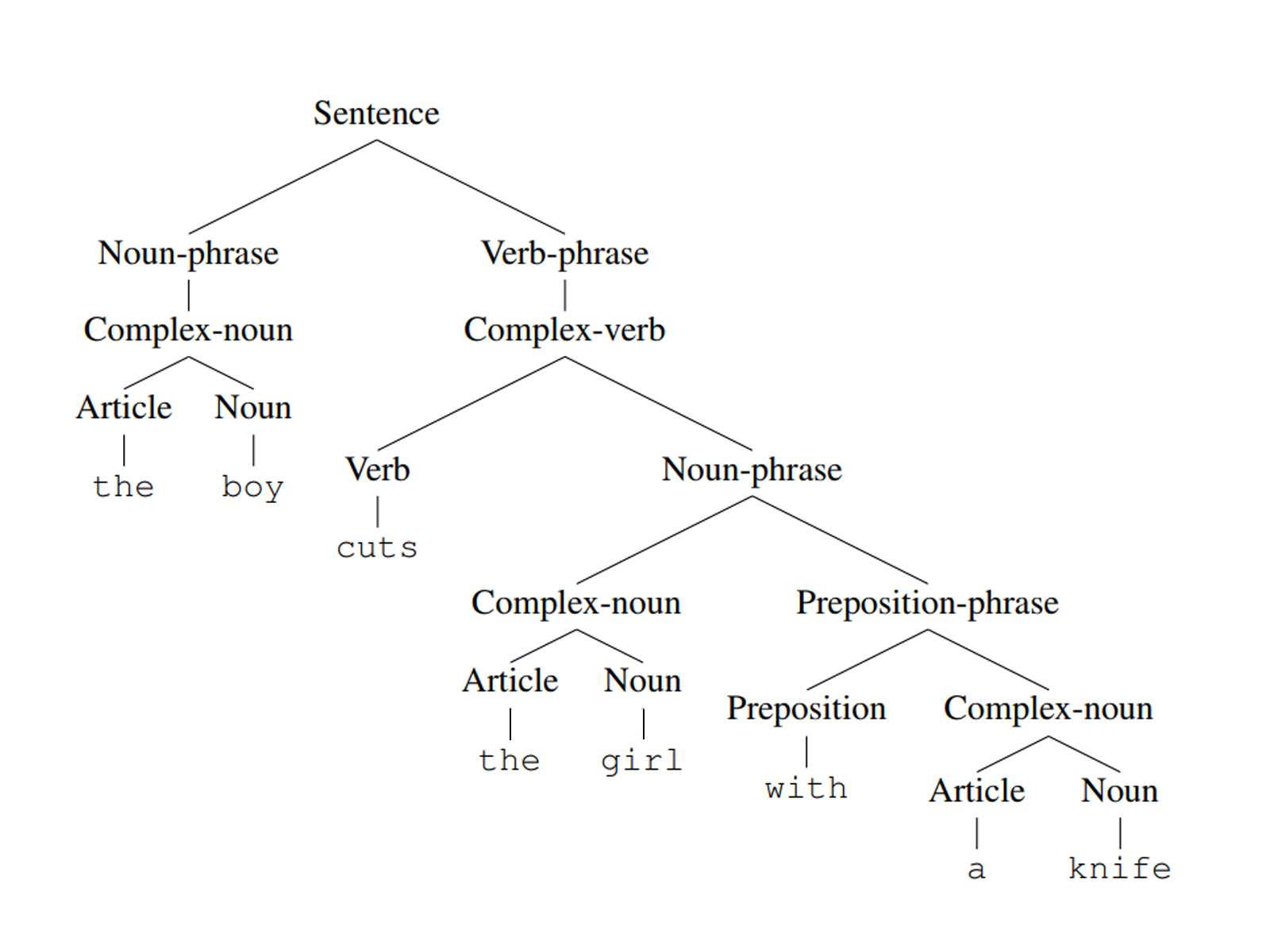
Revisit the opening example, how should we understand the boy cuts the girl with a knife?

• The boy uses a knife to cut a girl, or
• The girl with a knife is cut by the boy ?

One can construct a parse tree for a generated string to better understand its meaning. However, for the sentence above, we have two parse trees:

The boy uses a knife to cut a girl

The girl with a knife is cut by the boy

When a string has different parse tree structures, we say it is derived ambiguously in that grammar, the grammar is also said to be ambiguous.

Note that ambiguity concerns the structures of the parse trees, not the derivations. Different derivations may have the same tree structure. We call a derivation to be leftmost derivation if in each step we replace the leftmost variable. Each parse tree has exactly one leftmost derivation.

A language is called inherently ambiguous if it is only generated by ambiguous grammars.

Chomsky normal form

Definition: Chomsky normal form. A grammar is said to be in Chomsky normal form if each rule is one of the forms

where B, C are variables other than the start variable, a is a terminal. Also the rule \(S\rightarrow \epsilon\) is permitted when S is the start variable.

Theorem. Any grammar can be converted to Chomsky normal form

There are four steps to convert a grammar to its Chomsky normal form:

1. Introduce a new start variable \(S_0\) that links to the old start variable S by adding a rule \(S_0\rightarrow S\). This guarantees that in the new grammar, the start variable won’t appear on the right hand side of any rule.
2. Remove all rules of the form \(A\rightarrow\epsilon\), where \(A\neq S_0\). For each rule that has the form of \(B\rightarrow uAv\) where u and v are strings of variables and terminals, we add a rule \(B\rightarrow uv\). For example, if we have \(B\rightarrow uAvAw\) then we have to add \(B\rightarrow uvAw\ \vert\ uAvw\ \vert\ uvw\). If we have \(B\rightarrow A\), we add \(B\rightarrow\epsilon\) only under the condition that we haven’t deleted any rule \(B\rightarrow\epsilon\) yet, otherwise we won’t remove the \(\epsilon\)-rules completely.
3. Remove all unit rules that don’t concern with the start variable, i.e. rules of the form \(A\rightarrow B,\ A\neq S_0\). Then, whenever \(B\rightarrow u\) appears, where u is a string, we add a rule \(A\rightarrow u\) only under the condition that we haven’t deleted any rule \(A\rightarrow u\) yet (e.g. when u = B).
4. Remove all rules whose string sizes are larger than 2, e.g. \(A\rightarrow u_1u_2\dots u_k, k>2\) and \(u_i\) is either a terminal or a variable. After removing, add k-1 more rules: \(A\rightarrow u_1A_1\), \(A_1\rightarrow u_2A_2, \dots\), \(A_{k-2}\rightarrow u_{k-1}u_k\). For every \(u_i\) that is a terminal, we replace it with a new variable \(U_i\) and add a rule \(U_i\rightarrow u_i\).

Pushdown automata

(to be updated later - Mar 3, 2019)

Reference sources

1. Michael Sipser - “Introduction to the Theory of Computation” (3rd ed.)

Special thanks to Uyen Phuong for helping edit the images in this post.