So, what I implemented in this package is called “Generalized Region Growing.” You may have heard of Region Growing before. It has a close relationship with Breadth-First Search. This is an excerpted version of the manual of the package Generalized Region Growing, my work at GSoC 2018. I started this package and worked on it during the last three months under the supervision of Dr. Anisimov. I’m very excited to share you what I’ve done this summer!
The authors of this package are me, D. Anisimov, F. Lafarge, and S. Giraudot.
Introduction
This CGAL component implements the region growing algorithm for shape detection. The algorithm has been generalized to be working with any user-defined elements, connectivity method, and validity checking rules. Three types of detection are provided with the package:
- Plane detection in a 3D point cloud.
- Line detection in a 2D point set.
- Plane detection in a 3D mesh.
Other types of detection can also be added by the user.
Methods
Generalized region growing
The shapes are detected via the region growing approach, i.e. each region corresponds to a shape. The following steps are repeated:
- Pick the next available element (which could be a point, a face in a mesh, or any other user-defined type).
- Initialize a shape that contains this element and adheres to other properties of the element.
- Make this element the seed element and grow a region from here:
- Add the seed element to the region.
- Compute local neighborhood of this element with a connectivity method.
- Find in the neighborhoods the elements that are similar to the seed element, yet have not belonged to any shapes.
- Repeat step 3 for all neighbors that were found in step 3.3.
- Check the global condition on the region found. If it is true, the region is accepted to the region list, otherwise, the region is discarded and its elements are made available again for consideration in other shapes.
The customization for a generalized algorithm described above depends on the connectivity method, the similarity checking (“local condition”), and the global condition. Different types of elements have different approaches to these customizations and they will be discussed below.
Region growing with points
If the element type is point, the package provides two ways to search for the neighbors around an element:
-
Circular searching: The program creates a sphere (if the point is 3D) or a circle (if the point is 2D) with the query point being its center and the user-given radius. All points lie within this space will be regarded as the neighbors of this points.
-
k nearest neighbors searching: The program returns exactly k (given by the user) neighbors whose distances are closest to the query points.
For checking similarity between two points (one of them is already assigned to a region, while the other is still free) before pushing the free point to the region, the enclosing region of the assigned point is also taken into consideration. The program associates the region to a best-fit hyperplane (2D line or 3D plane), using the least square method. If the distance from the free point to the hyperplane is within a user-defined value, and the dot product between the normal of the free point and the normal of the hyperplane is large enough, the local condition will be true.
The global condition simply checks if the size of a region is larger than a specified value. The size of the region is the number of elements it contains.
Region growing with mesh
If the element type is face in a mesh, the neighbors of a face can be retrieved by selecting all faces that share an edge with the query face. Local condition in this case is very similar to the 3D point case: the faces are broken down to their vertices and a plane are associated with them. However, the distance from a face to the fit plane is simplifed down to the distance from the centroid of the face. Vertices do not need normals linked with them, instead, the normal of a face is calculated from its any three points; and the dot product between a face’s normal and the fit plane’s normal is computed as usual.
The global condition simply checks if the region is a non-empty list.
Parameters
The class CGAL::Region_growing::Generalized_region_growing is templated by three parameter classes, namely Traits class, Connectivity class, and Conditions class, subsequently described as follows.
Traits
Traits class gathers all necessary types needed for the detection:
Input_range: AnIterator_rangeof bidirectional iterator. This pair of iterators define the begin iterator and the past-the-end iterator of a container.ElementMap: Since the input may contain the elements and their properties (e.g. points and normals associated with them), it is necessary to provide anLvaluePropertyMapthat maps to the elements.Kernel_: The user must also provide a kernel to perform calculations.
From those types, the following types are deduced across the package:
Element: Equivalent toElementMap::value_type.Element_with_properties: Equivalent toElementMap::key_type.
Connectivity
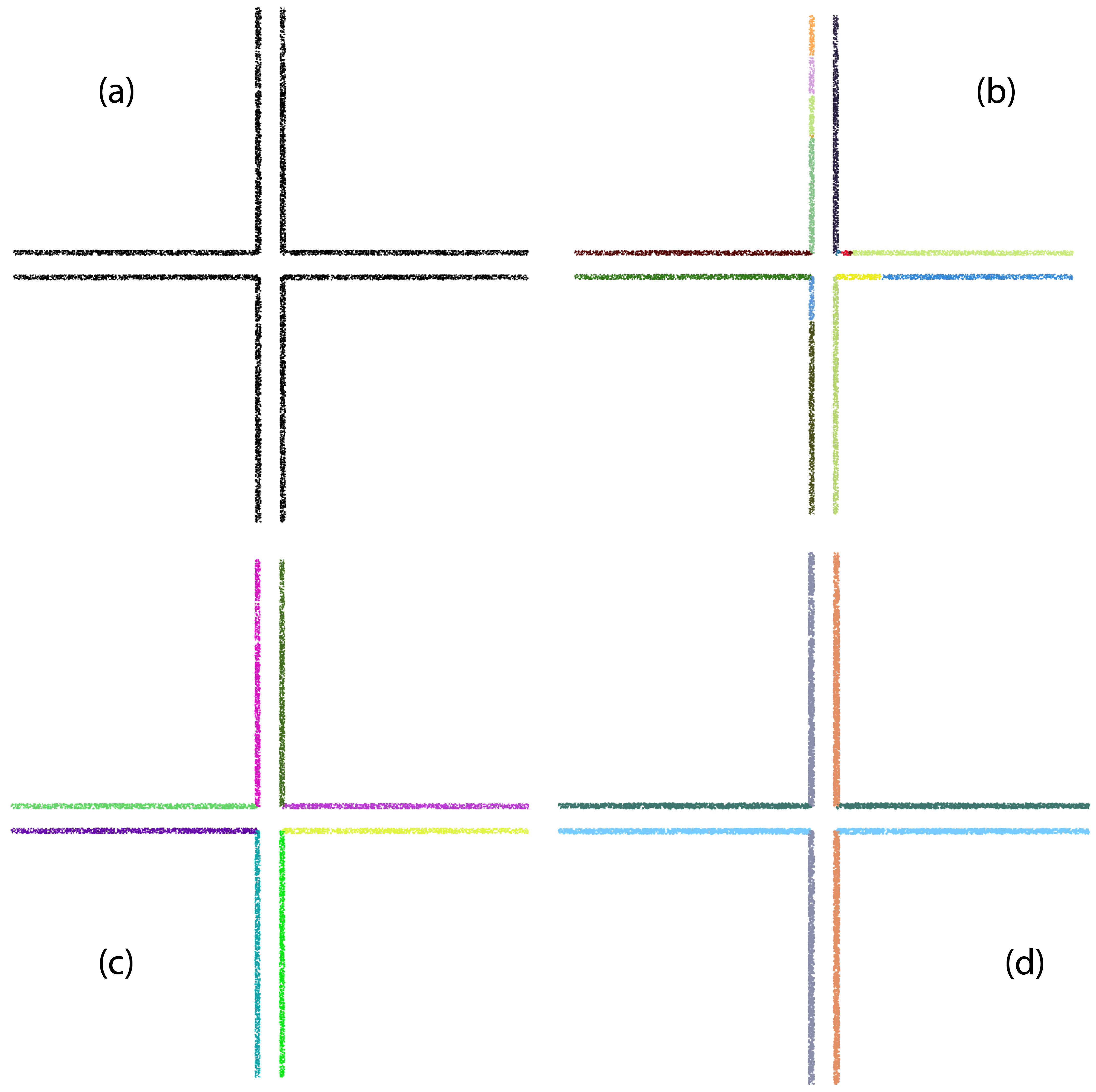
The effect of radius
(a) Input 2D point set
(b) 17 regions found when radius = 0.1
(c) 8 regions found when radius = 0.3
(d) 4 regions found when radius = 1.2
When searching for neighbors of an element, the only parameter needed is that query element. However, in the construction of the class Connectivity, each method requires different parameters:
-
Circular searching (on points): The user must provide the
radiusof the hypersphere defining the neighborhood space. -
k nearest neighbors searching (on points): The user must provide the
number_of_neighborsreturned in each search query. -
Neighbor faces searching (on mesh): The user must provide the mesh that defines the connection between its faces.
In the case of point, choosing the radius or number_of_neighbors plays an important role in producing a good result. If radius is too large, there will be less regions, and the details are not clearly separated. Meanwhile, if radius is too small, there will be more regions, and the point set may be oversegmented. Consider a 2D map at an intersection in a city as in \cgalFigureRef{Generalized_region_growing_radius}. Each region is painted with a unique color. As radius increases, the details become less clear. When radius = 0.3 (c), the best visualization is produced.
Conditions
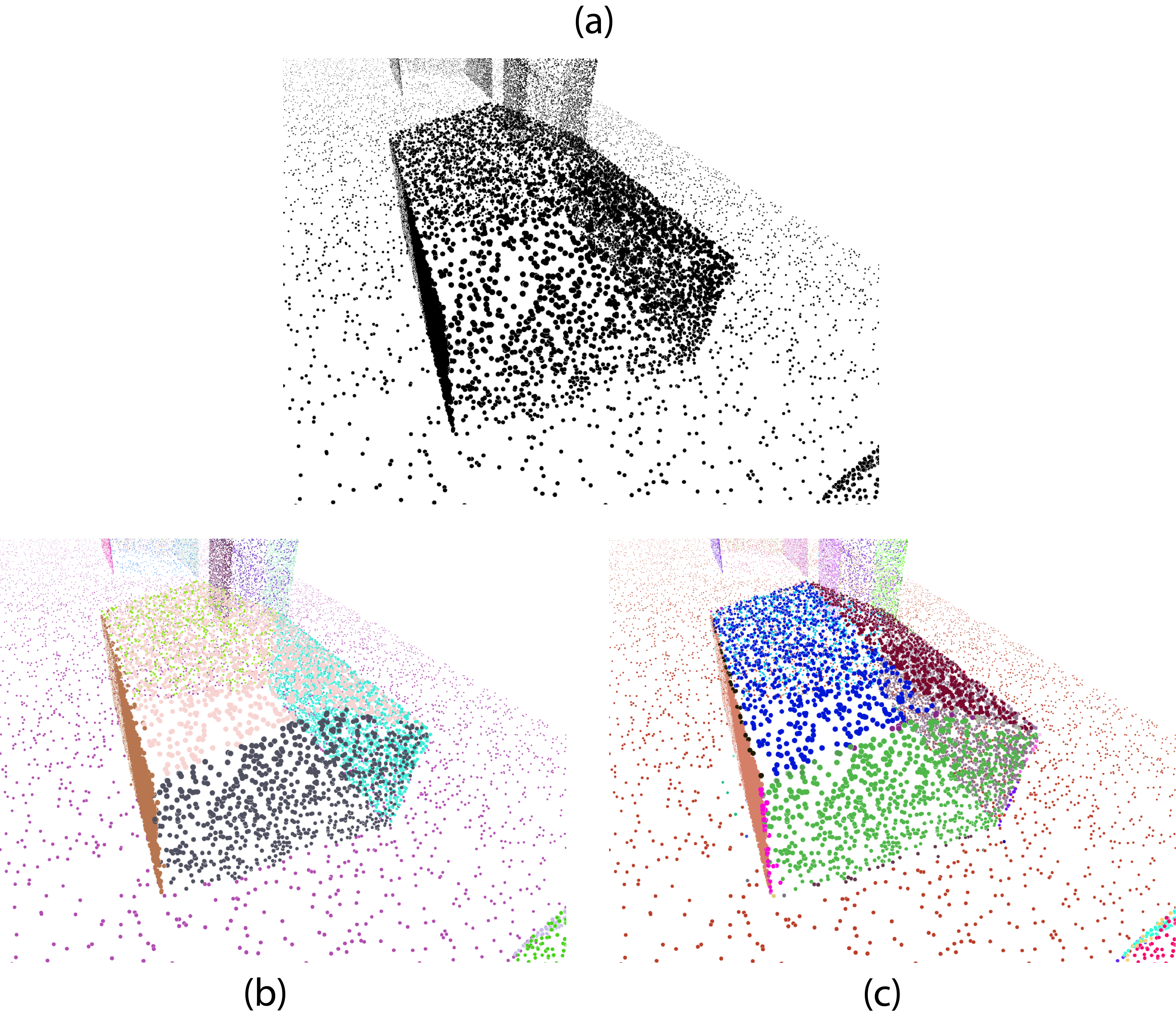
The effect of normal threshold
(a) Input 3D point cloud
(b) Result when normal_threshold = 0.5
(c) Result when normal_threshold = 0.9
The Conditions classes for points and mesh work alike, which require:
epsilon: the maximum Euclidean distance allowed from the element to the hyperplane.normal_threshold: the minimum dot product allowed between the normal of the element and the normal of the hyperplane.min_region_size(only when working with points): the minimum number of elements that a region must have.mesh(only when working with mesh): the mesh providing the vertices around a face, so its normal and centroid can be calculated.
Similar to the searching size in the Connectivity class, the choice of normal_threshold and epsilon is also important. Figure \cgalFigureRef{Generalized_region_growing_normal_threshold_diff} shows the roof top of the house can be distinguished as two planes (painted in blue and dark red) when the threshold is strict enough (c), or it can be recognized as only one plane (painted in pale yellow) in the other setting (b).
Customization
As once mentioned, this package can be customized in various ways to work with different kinds of element and shape. However, some concepts are set up so that the program can run successfully.
The class CGAL::Region_growing::Generalized_region_growing is templated by three classes: Traits, Connectivity, and Conditions. The Traits class provided in the package – CGAL::Region_growing::Region_growing_traits is sufficient to define the types that are going to be used, hence will not be discussed here. The other two classes may differ in many ways. For example, the user does not want to use Euclidean distance but to use a Manhattan distance, these classes will have to be re-written. Please refer to the concepts RegionGrowingConnectivity and RegionGrowingConditions to see the requirements of the classes.
Performance
The main parameter that affects the region growing algorithm is the neighborhood size (radius or number_of_neighbors) at each retrieval. Larger neighbor lists are often followed by smaller number of regions, larger coverage (the ratio between the number of points assigned to some region and the total number of points given in the input), and longer running time. On a test of 67768 points, the following table is produced:
radius | Time (in seconds) | Number of regions | Number of assigned points |
|---|---|---|---|
| 1 | 0.832657 | 796 | 4491 |
| 3 | 0.837602 | 3054 | 63154 |
| 6 | 0.95962 | 2483 | 64977 |
| 9 | 1.13608 | 2282 | 65353 |
If the neighborhood size is set too low, some points may be isolated and the region size is not large enough, hence will be discarded. This not only causes latency in the program, but also reduces the coverage value, as can be seen when radius = 1.
…
Thank you for reading down to here. I will soon post my GSoC stories, hopefully they may help other students who have interests and stumble upon my site.
::cheerfully smile::

