Hồi đó mình đi cắm trại, tham gia trò chơi lớn, thường có một trò “giải mật thư.” Khi nhận mật thư, kèm với thư đã mã hóa (ciphertext) là một dòng văn bản “gợi ý” cách giải mã.
Ví dụ, “gợi ý” đưa ra là:
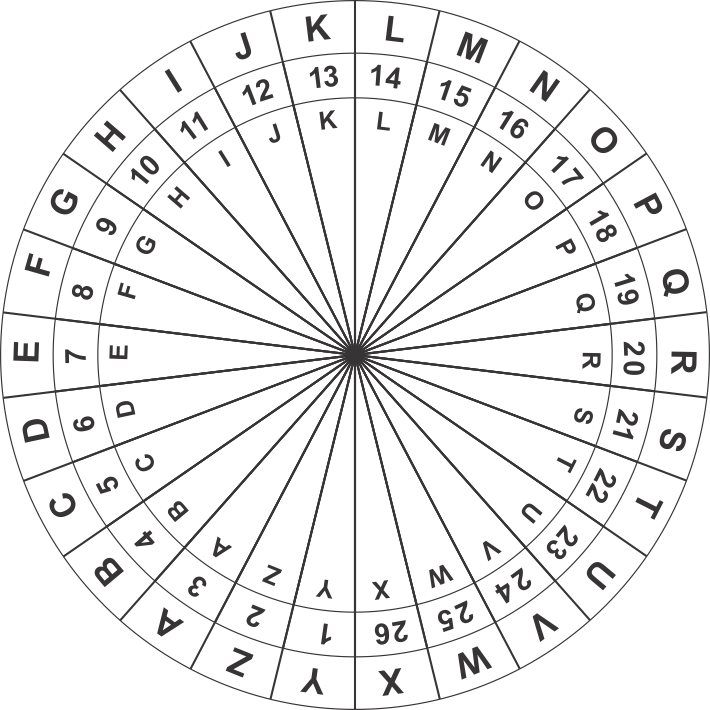
"Tuổi 17 bẻ gãy sừng trâu."
Theo văn hóa thể thao nước mình, trong các giải đấu dành cho vận động viên 17 tuổi, thì người ta gọi là “giải đấu U17.” Như vậy, ký tự “U” trên bảng chữ cái tương ứng với số 17. Lúc này, học sinh mới xoay hai vòng tròn bên trong sao cho số 17 khớp với chữ U ở vòng tròn ngoài cùng. Và ta có bảng đối chiếu, ví dụ chữ U trong cipher text sẽ đổi thành chữ O, hoặc chữ V thì được đổi thành P.
Tóm lại, ý tưởng của mã hóa Cipher là chọn ra một số nguyên \(k\) làm khóa và một tập hợp \(\mathbb{Z}_n\). Số \(x\in \mathbb{Z}_n\) sẽ được mã hóa theo hàm sau:
\[E: \mathbb{Z}_n \rightarrow \mathbb{Z}_n\\ x \mapsto (x+k)\text{ mod }n\]Việc giải mã sẽ rất đơn giản nếu biết \(k\).
\[D: \mathbb{Z}_n \rightarrow \mathbb{Z}_n\\ y \mapsto (y-k)\text{ mod }n\]Multiplicative cipher là phép mã hóa tương tự như Caesar cipher, tuy nhiên thay vì cộng với \(k\), ta lại nhân:
\[E: \mathbb{Z}_n \rightarrow \mathbb{Z}_n\\ x \mapsto (xk)\text{ mod }n\]Mã hóa nhân bảo mật hơn mã hóa Caesar ở chi phí tìm nghịch đảo modulo:
\[D: \mathbb{Z}_n \rightarrow \mathbb{Z}_n\\ y \mapsto (yk^{-1})\text{ mod }n\]Cả hai phép mã hóa đều dễ bị phá trong trường hợp \(n\) nhỏ, bằng cách thử mọi giá trị của \(k\). Nhưng mã hóa nhân đòi hỏi phải tính nghịch đảo modulo của \(k\) theo \(n\), chứ không cộng trừ thẳng thừng như mã hóa Caesar.
Tuy nhiên, dù cho cách nào thì hai phương pháp mã hóa này đều phải dùng chung khóa \(k\). Tức là nếu Bob muốn gửi cho Alice một tin nhắn mà không muốn bên trung gian thứ ba (attacker) biết được, dù cho hắn có lấy được tin, thì Bob và Alice phải cùng biết khóa \(k\). Phương pháp mã hóa - giải mã dựa trên cùng một khóa \(k\) được gọi là mã hóa đối xứng (symmetrical cryptography). Bên mã hóa và bên giải mã phải biết cùng một khóa bí mật.
Vấn đề đặt ra ở đây là, làm sao Bob với Alice cùng biết khóa \(k\)? Bob không thể “nhắn tin” gửi Alice khóa \(k\) vì điều đó làm cho việc mã hóa trở nên vô nghĩa. Họ phải gặp mặt nhau. Ngay cả như vậy cũng không cải thiện độ bảo mật của phương pháp này tí nào.
Nói lạc đề một tí, ngày xưa trong chiến tranh, Đức Quốc xã có sử dụng cỗ máy Enigma để mã hóa và giải mã thông tin. Người Đức cho rằng đây là cỗ máy không thể hack được. Các bạn có thể xem thêm về cỗ máy Enigma tại đây.
Tuy nhiên, Enigma lại hoạt động dựa trên phương pháp mã hóa đối xứng. Dù người Đức đã thay đổi khóa mỗi ngày, nhưng Alan Turing đã tìm ra được nguyên tắc đó và giải mã được các mật thư mà người Đức gửi cho nhau. (Cái này xem trên phim The Imitation Game)
Như vậy, phương pháp mã hóa đối xứng khá là nguy hiểm vì phải có một cách đề Alice nói cho Bob biết chìa khóa chung để mã hóa và giải mã. Khả năng rất cao là attacker có thể chen ngang cuộc trò chuyện này và biết được.
Hơn nữa, nếu Alice là một người quan trọng, cần phải nhận thư từ hàng trăm người, cô lại phải giữ hàng trăm chìa khóa khác nhau. Điều này tỏ ra rất bất tiện.
Một cách hiệu quả hơn là thay vì Alice và Bob giữ hai chìa khóa y hệt nhau để mã hóa (hoặc giải mã) thì Alice sẽ giữ một chìa khóa duy nhất cho mình (private key) và “bán” ổ khóa (public key) cho những ai muốn gửi thư cho mình. Bob sẽ lấy ổ khóa đó và mã hóa bức thư, rồi gửi ciphertext cho Alice. Alice mới dùng chìa khóa mà chỉ có mình cô sở hữu để giải mã bức thư. Như vậy, sẽ không có sự trao đổi thông tin bí mật giữa bên gửi và bên nhận. Mặt khác, Alice có thể nhận thư một cách bảo mật từ bất cứ ai mà không cần phải quản lý nhiều chìa khóa. Phương pháp này gọi là asymmetrical cryptography (mã hóa bất đối xứng), hay còn gọi là public-key cryptography (mã hóa khóa công cộng).
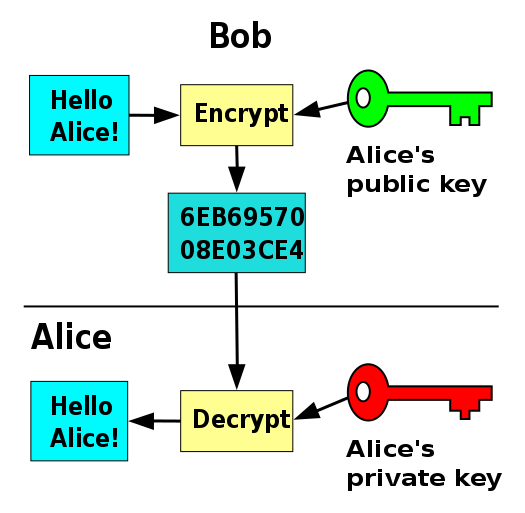
Sơ đồ public-key cryptography (Nguồn: Wikipedia)
Với ý tưởng mã hóa này, đòi hỏi hàm mã hóa \(E\) phải đủ phức tạp để khó có thể tìm ra hàm giải mã \(D\). Đồng thời, phải có cách để giải mã dựa trên cách xây dựng hàm \(E\), mà cách giải mã chỉ có Alice nắm được.
Mã hóa RSA được thiết kế bởi ba nhà toán học Ron Rivest, Adi Shamir, và Leonard Adleman, được công bố lần đầu tiên vào năm 1977 và vẫn còn được sử dụng đến tận ngày hôm nay.
Quá trình mã hóa được thực hiện như sau:
- Chọn hai số nguyên tố lớn \(p\) và \(q\) (hai số này được giữ bí mật, chỉ Alice biết), tích của chúng là \(n=pq\).
- Ta có thể tính được phi hàm Euler của số \(n\) dựa trên \(p\) và \(q\), tức là \(\varphi(n)=(p-1)(q-1)\). Một số nguồn dẫn sử dụng hàm Carmichael.
- Chọn một số \(e\in \mathbb{Z}_{\varphi(n)}\) làm public key sao cho \(\text{GCD}(e,\varphi(n))=1\).
- Hàm mã hóa:
- Tính số \(d \equiv e^{-1}\pmod{\varphi(n)}\). Số \(d\) này là private key dùng để giải mã.
- Hàm giải mã:
Sau đây là phần chứng minh phép giải mã như trên là đúng.
Để chứng minh việc giải mã và mã hóa là thống nhất với nhau ta phải chứng minh chuỗi biến đổi sau là đúng:
\[y \overset{D}{\longmapsto} y^d \text{ mod } n \overset{E}{\longmapsto} y\]Tức là chứng minh \((y^d \text{ mod } n)^e \text{ mod } n = y\) hay \(y^{ed}\equiv y\pmod{n}\)
Ta có:
\[\begin{aligned} & ed \equiv 1\pmod{\varphi(n)}\\ \Rightarrow & ed-1 = k\varphi(n)=k(p-1)(q-1)\\ \end{aligned}\]Theo định lý Fermat nhỏ:
\[\begin{aligned} & y^{p-1}\equiv 1 \pmod{p}\\ \Rightarrow & \left(y^{p-1}\right)^{q-1}\equiv 1^{q-1}\equiv 1\pmod{p}\\ \Rightarrow & \left(y^{(p-1)(q-1)} - 1\right)\vdots p \end{aligned}\]Chứng minh tương tự, ta cũng có:
\[\left(y^{(p-1)(q-1)} - 1\right)\vdots q\]Vì \(p\) và \(q\) là hai số nguyên tố cùng nhau (thực ra chúng là hai số nguyên tố khác nhau luôn rồi) nên suy ra:
\[\begin{aligned} & \left(y^{(p-1)(q-1)} - 1\right)\vdots (pq)\\ \Rightarrow & y^{(p-1)(q-1)} \equiv 1 \pmod{pq=n}\\ \Rightarrow & y^{k(p-1)(q-1)} \equiv 1^k \equiv 1 \pmod{n}\\ \Rightarrow & y^{ed-1} \equiv 1 \pmod{n}\\ \Rightarrow & y^{ed} \equiv y \pmod{n} \text{ (QED) } \end{aligned}\]Tất cả những gì Bob biết là số \(n\) và \(e\) để thực hiện phép tính \(y = x^e \text{ mod } n\) với \(x\) là tin nhắn cần mã hóa. Attacker nếu có trong tay \(n\), \(e\), và \(y\) cũng khó có thể giải ra được \(x\) nếu không có trong tay số \(d\). Thấy rằng các số liệu này đều được xây dựng từ hai số nguyên tố \(p\) và \(q\) ra cả, nhưng chú ý là thời gian để phân tích một số nguyên tố \(n\) ra thừa số nguyên tố sẽ vô cùng tốn kém! Phép cộng, trừ, nhân các số nguyên rất lớn, khoảng 150 chữ số chẳng hạn, có thể được tính bằng máy tính rất nhanh trong vòng chưa đầy 1 giây, nhưng để phân tích một số \(n\) có 150 chữ số ra thừa số nguyên tố thì phải tốn nhiều năm liền. Nếu không có trong tay \(p\) và \(q\) sẽ không tính được \(\varphi(n)\), và hiển nhiên, không thể tính được \(d \equiv e^{-1} \pmod{\varphi(n)}\), chìa khóa để giải mã.
Tuy nhiên, đã có nhiều nghiên cứu để phá vỡ RSA. Chính vì vậy, ngày nay RSA được dùng kết hợp với một số thuật toán mã hóa khác để an toàn hơn. Dù sao thì RSA vẫn là cốt lõi của nhiều nền tảng bảo mật hiện nay. RSA còn được ứng dụng trong e-signature (chữ ký điện tử), trong đó private key dùng để sinh ra chữ ký dựa trên văn bản cần ký, còn public key dùng để kiểm tra xem chữ ký đó và văn bản đó có khớp nhau hay không.