Hồi còn học phổ thông thì phần lớn các bạn được tiếp cận với hàm một biến, người ta hay viết \(y=f(x)\) thì \(x\) gọi là biến độc lập và \(y\) gọi là biến phụ thuộc. Ví dụ trong sách vật lý 10, mấy bài đầu có dạy về chuyển động thẳng đều, công thức là \(x = x_0 + v_0t\) thì đây chẳng qua là hàm tính độ dời (\(x\), biến phụ thuộc) theo thời gian (\(t\), biến độc lập). Giả sử xét bài toán ngược là \(t = \frac{x-x_0}{v_0}\) thì lúc này \(t\) lại là biến phụ thuộc. Đó là giới thiệu sơ qua về hàm số, cái khái niệm rất lạ mà cũng rất quen. :))
Nhưng mà trong thế giới thực thì hiếm có khi nào bạn thu thập dữ liệu của một đại lượng mà cho ra được kết quả. Một hàm không chỉ dừng lại ở mức độ “từ một số biến đổi thành một số”, mà còn có thể là “từ nhiều số biến đổi thành một số”, “từ một số biến đổi thành nhiều số”, “từ nhiều số biến đổi thành nhiều số”, … Ví dụ nhé:
- Xe chuyển động thẳng đều, tôi biết trước \(x_0\) và \(v_0\), bây giờ bạn cho tôi bao nhiêu thời gian \(t\) tính từ khi xe xuất phát thì tôi trả cho bạn bấy nhiêu giá trị \(x\) tương ứng. Đó là hàm biến đổi “từ một số thành một số” (scalar-scalar). Lưu ý \(x_0\) và \(v_0\) là hằng số, không tham gia vào chuyện biến đổi ở đây nhé.
- Xe bây giờ không còn chuyển động trên đường thẳng nữa mà chuyển động trên mặt phẳng tọa độ \(Oxy\), vận tốc của xe được tính qua một hàm nào đó, gọi là \(v=f(x,y)\), lúc này \(f\) sẽ là hàm biến đổi “từ nhiều số thành một số” (vector-scalar). Các thông số đưa vào hàm có thể được mô phỏng qua vector.
- Xe di chuyển trên một đường thẳng nhưng tại mỗi vị trí khác nhau trên chuyến đi, trạng thái của xe được ghi lại bao gồm số hành khách trên xe \(u\) và… lượng xăng còn lại \(v\) trong bình chẳng hạn (ví dụ tệ vl), nhưng cơ bản là ta sẽ có hàm \(f(x) = \left[\begin{array}{c}u\\ v\end{array}\right]\), nhận vào một số và trả về nhiều số.

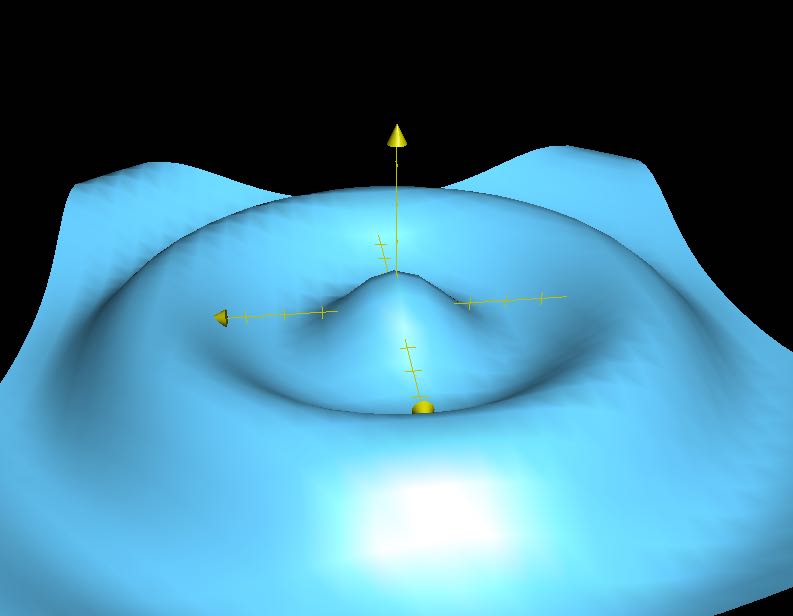
What are the equations for this type of surface? Source: Reddit
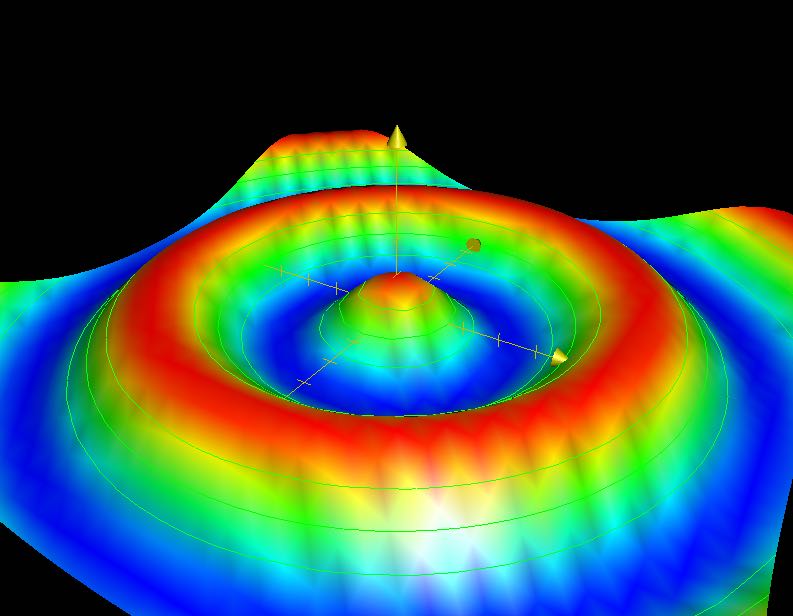
Thì cái bức tường này, người ta có thể mô phỏng sơ sơ thông qua cái hàm \(z=\cos(\sqrt{x^2+y^2})\). Hàm này có hình dạng như sau:
Ờm, nhìn cũng… hơi giống. Nói chung đưa vô hai hình này để cho các bạn thấy Math luôn ở quanh ta thôi, warm up tí :))
Okay thì đó cũng là một dạng hàm vector-scalar. Cho biết tọa độ của bức tường, hàm này sẽ cho bạn biết vị trí đó cần nhô lên bao nhiêu centimeter chẳng hạn.
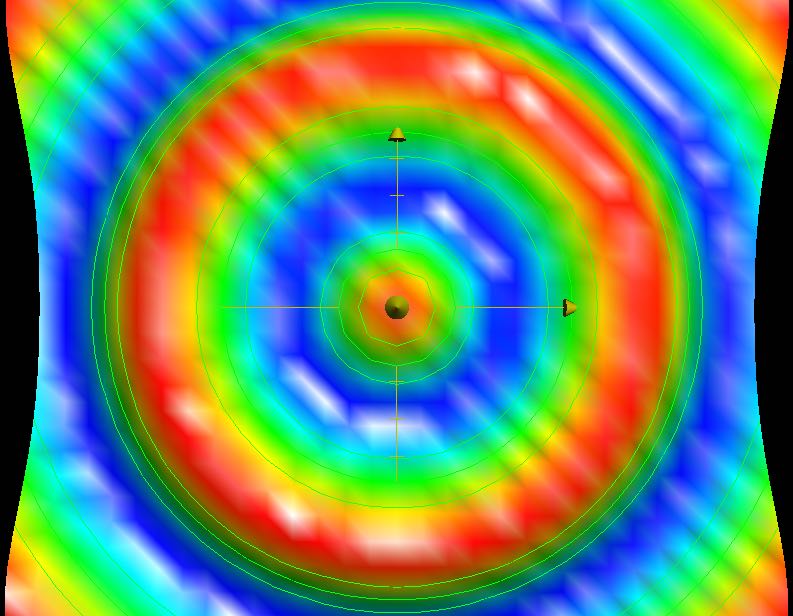
Ngoài cách mô phỏng đó, còn có cách dùng đường mức (contour lines) giống như trong địa lý. Khi nhìn từ trên cao xuống hình trên:
Các đường cong khép kín biểu thị cùng một độ cao. Trong hình trên, phần nào càng đỏ thì càng cao, càng xanh dương thì càng thấp, hai đường cong màu xanh lá cây liên tiếp nhau lệch nhau 0.5 đơn vị độ cao.
Đối với các hàm vector-vector, sao cho biến độc lập và biến phụ thuộc có cùng số chiều, chẳng hạn input vào \(x,y,z\) thì cho ra phải đủ ba số \(x',y',z'\), người ta còn có thể biểu diễn qua trường vector (vector fields). Ví dụ như đổ nước lên mặt phẳng \(Oxy\), tại mỗi điểm \((x,y)\) trên mặt phẳng, các giọt nước sẽ có xu hướng di chuyển theo vector \((2,3)\), trường vector lúc này có dạng:
Mỗi điểm trên mặt phẳng đều có một vector dính với nó, và tất cả vectors này đều bằng \((2,3)\). Để cho đỡ rối rắm, trong hình độ dài của các vector này không bằng \(\sqrt{2^2+3^2}=3.6\) mà chỉ một đoạn nhỏ, và các vector được bố trí thưa ra. Trên thực tế, mọi điểm li ti trên mặt phẳng này đều có một vector \((2,3)\) dính với nó.
Trường vector trên được ký hiệu qua công thức toán học như sau:
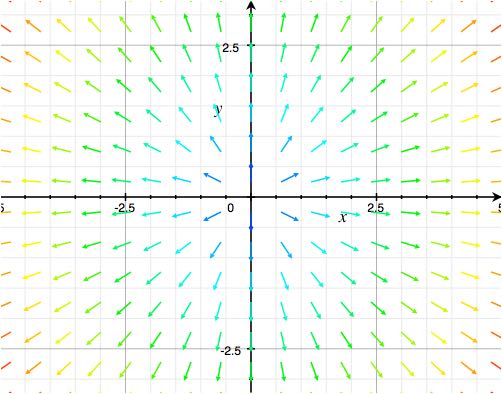
\[\Delta\left[\begin{array}{c}x\\ y\end{array}\right] = \left[\begin{array}{c}2\\ 3\end{array}\right]\]Trong hình sau, mọi điểm \((x,y)\) đều được gắn một vector \((x,y)\). Màu sắc của vector biểu thị độ lớn của nó: xanh nhỏ hơn đỏ. Ví dụ ở điểm \((1,1)\) thì có vector \((1,1)\) gắn vào, ở điểm \((2.5, 2.5)\) thì có vector \((2.5, 2.5)\) gắn vào, quan sát hướng vector để hiểu rõ hơn.
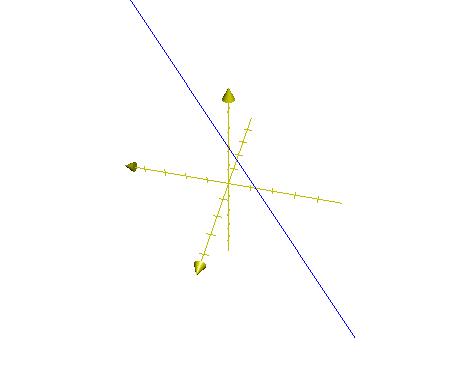
\[\Delta\left[\begin{array}{c}x\\ y\end{array}\right] = \left[\begin{array}{c}x\\ y\end{array}\right]\]Bạn còn nhớ “phương trình tham số” của đường thẳng trên mặt phẳng và trong không gian hồi năm lớp 10 hay không?
\[\begin{cases} x = t y = t + 3 z = 3t + 6 \end{cases}\]Tại sao phương trình này lại mô phỏng đường thẳng? Vì khi thay mọi giá trị thực \(t\), ta sẽ có vô số điểm, và chúng đều tập trung trên một đường thẳng. Điều tương tự cũng xảy ra với các phương trình tham số khác.
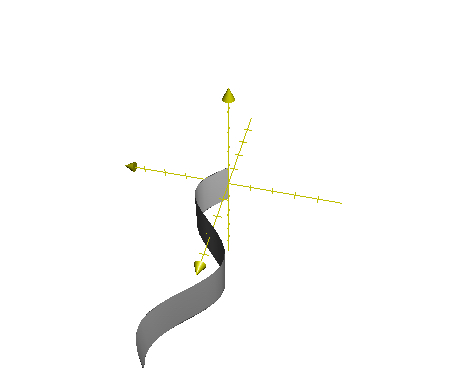
\[\begin{cases} x = \sin(t)\\ y = t\\ z = \cos(t)\\ \end{cases}\] \[\begin{cases} x = \sin(t)\\ y = t\\ z = \cos(u)\\ \end{cases}\]Mặt phẳng trong hình trên kéo dài vô tận, vì khi đẩy giá trị \(t\) đi xa dần thì lại càng có nhiều điểm mới được sinh ra, kéo dài đến vô cùng. Còn trong phương trình sau, các tham số dù có trải dài đến đâu cũng bị giới hạn lại bởi hàm lượng giác tuần hoàn.
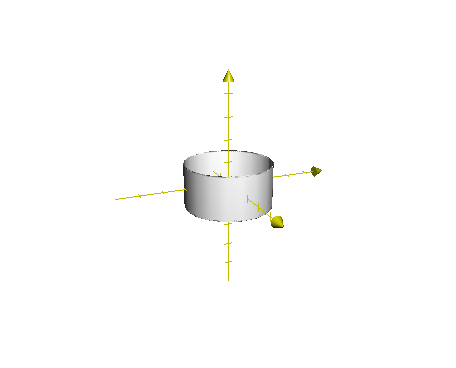
\[\begin{cases} x = 2\sin(t)\\ y = 2\cos(t)\\ z = \cos(u)\\ \end{cases}\]Đó là tổng quan về hàm đa biến, một bài viết nhỏ để khởi động các kiến thức thú vị sau này. :v