Hồi quy tuyến tính là một phương pháp tìm quan hệ tuyến tính giữa những biến số độc lập (independent variables) với một biến số phụ thuộc (dependent variable).
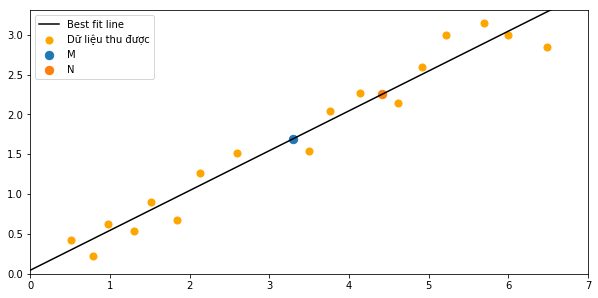
Chẳng hạn, một cái máy theo dõi quãng đường của một chiếc xe chuyển động thẳng đều. Tại một \(n\) thời điểm \(t_i\), nó ghi lại xem xe đã đi được bao nhiêu mét (ký hiệu là \(s_i\)). Nhưng bạn biết thì thế giới thực chẳng bao giờ hoàn hảo được cả, máy đo có thể bị sai số do nguồn điện, đường xóc, vật cản, … Và kết quả khi biểu diễn \(n\) lần đo đó lên đồ thị, ta có hình sau (quan sát các điểm biểu diễn màu cam):

Minh họa hồi quy tuyến tính. Trục tung là đại lượng độ dài đi được, trục hoành là đại lượng thời gian.
Công việc của bạn là “chuẩn hóa” lại dữ liệu bị nhiễu này. Công việc chuẩn hóa có thể có nhiều mục đích, ví dụ như để tính vận tốc của xe, hoặc để dự đoán trong tương lai ở thời điểm \(t_{n+1}\) thì xe đã di chuyển được bao xa.
Bạn biết rằng đồ thị \(s\)-\(t\) của vật chuyển động thẳng đều thì có đường thẳng (tuyến tính). Một trong những phương pháp phổ biến để phân tích quan hệ tuyến tính giữa hai đại lượng như quãng đường và thời gian trong bài toán này là hồi quy tuyến tính bằng phương pháp bình phương tối thiểu.
Ý tưởng chính của phương pháp hồi quy tuyến tính là tìm ra đường thẳng như trong hình (gọi là best fit line), sao cho tổng bình phương của độ dài các đoạn màu xanh dương là nhỏ nhất.
Để cho tổng quát, mình sẽ ký hiệu \(y\) là quãng đường đo được (thay cho \(s\)), còn \(x\) là thời điểm đo (thay cho \(t\)).
Từ tọa độ các điểm \((x,y)\) cho trước trên mặt phẳng, hãy lập bảng sau:
| \(x\) | \(y\) | \(x^2\) | \(y^2\) | \(xy\) | |
|---|---|---|---|---|---|
| 6 | 3 | 36 | 9. | 18. | |
| 0.98 | 0.63 | 0.9604 | 0.3969 | 0.6174 | |
| 1.84 | 0.67 | 3.1856 | 0.4489 | 1.2328 | |
| 2.13 | 1.27 | 4.5369 | 1.6129 | 2.7051 | |
| 2.6 | 1.52 | 6.76 | 2.3104 | 3.952 | |
| 3.5 | 1.54 | 12.25 | 2.3716 | 5.39 | |
| 3.76 | 2.04 | 14.1376 | 4.1616 | 7.6704 | |
| 4.14 | 2.27 | 17.1396 | 5.1529 | 9.3978 | |
| 4.61 | 2.14 | 21.2521 | 4.5796 | 9.8654 | |
| 1.51 | 0.9 | 2.2801 | 0.81 | 1.359 | |
| 1.3 | 0.54 | 1.69 | 0.2916 | 0.702 | |
| 4.91 | 2.59 | 24.1081 | 6.7081 | 12.7169 | |
| 5.21 | 3 | 27.1441 | 9. | 15.63 | |
| 5.69 | 3.15 | 32.3761 | 9.9225 | 17.9235 | |
| 6.48 | 2.84 | 41.9904 | 8.0656 | 18.4032 | |
| 0.79 | 0.22 | 0.6241 | 0.0484 | 0.1738 | |
| 0.51 | 0.42 | 0.2601 | 0.1764 | 0.2142 | |
| Avg | 3.292 | 1.691 | 14.5232 | 3.8269 | 7.49029 |
Sau đó bạn vẽ một đường thẳng đi qua điểm \(M(\overline{x}, \overline{y})\) và điểm \(N\left(\frac{\overline{x^2}}{\overline{x}}, \frac{\overline{xy}}{\overline{x}}\right)\) sẽ ra được best fit line. Với bảng kết quả trên, mình có được \(M(3.292, 1.691)\), \(N(4.412, 2.251)\), và \(\hat{y} = f(x) = 0.5a + 0.044\).
Kết quả:
Để hiểu được các phân tích sau, các bạn cần phải có kiến thức cơ bản về các chủ đề sau:
- Đạo hàm hàm một biến (derivative);
- Đạo hàm hàm nhiều biến (multi-variable derivative), tích phân ma trận (matrix calculus), nhân ma trận.
Không cần học ngay bây giờ đâu! Các bạn cứ đọc đến đâu tìm hiểu đến đó là được.
Nếu giả sử best fit line có phương trình là:
\[\hat{y} = f(x) = ax+b\]thì tại mỗi thời điểm đo \(t\), độ dài đoạn màu xanh là \(\lvert\hat{y} - y\rvert\). Tổng bình phương độ dài các đoạn màu xanh là:
\[g(a, b) = \color{red}(y_1 - \hat{y}_1)^2 \color{black}+ \color{green}(y_2 - \hat{y}_2)^2 \color{black}+ ... + \color{blue}(y_n-\hat{y}_n)^2\] \[g(a, b) = \color{red}(y_1 - ax_1-b)^2 \color{black}+ \color{green}(y_2 - ax_2-b)^2 \color{black}+ ... + \color{blue}(y_n-ax_n-b)^2\]Nhắc lại rằng các số \(x_1, y_1, x_2, y_2, ...\) đã được biết trước qua hàng loạt kết quả đo (tọa độ của các điểm màu cam). Mục tiêu của chúng ta là tìm các giá trị \(a,b\) sao cho \(g(a,b)\) đạt giá trị nhỏ nhất.
Tiếp tục biến đổi hàm \(g(a,b)\):
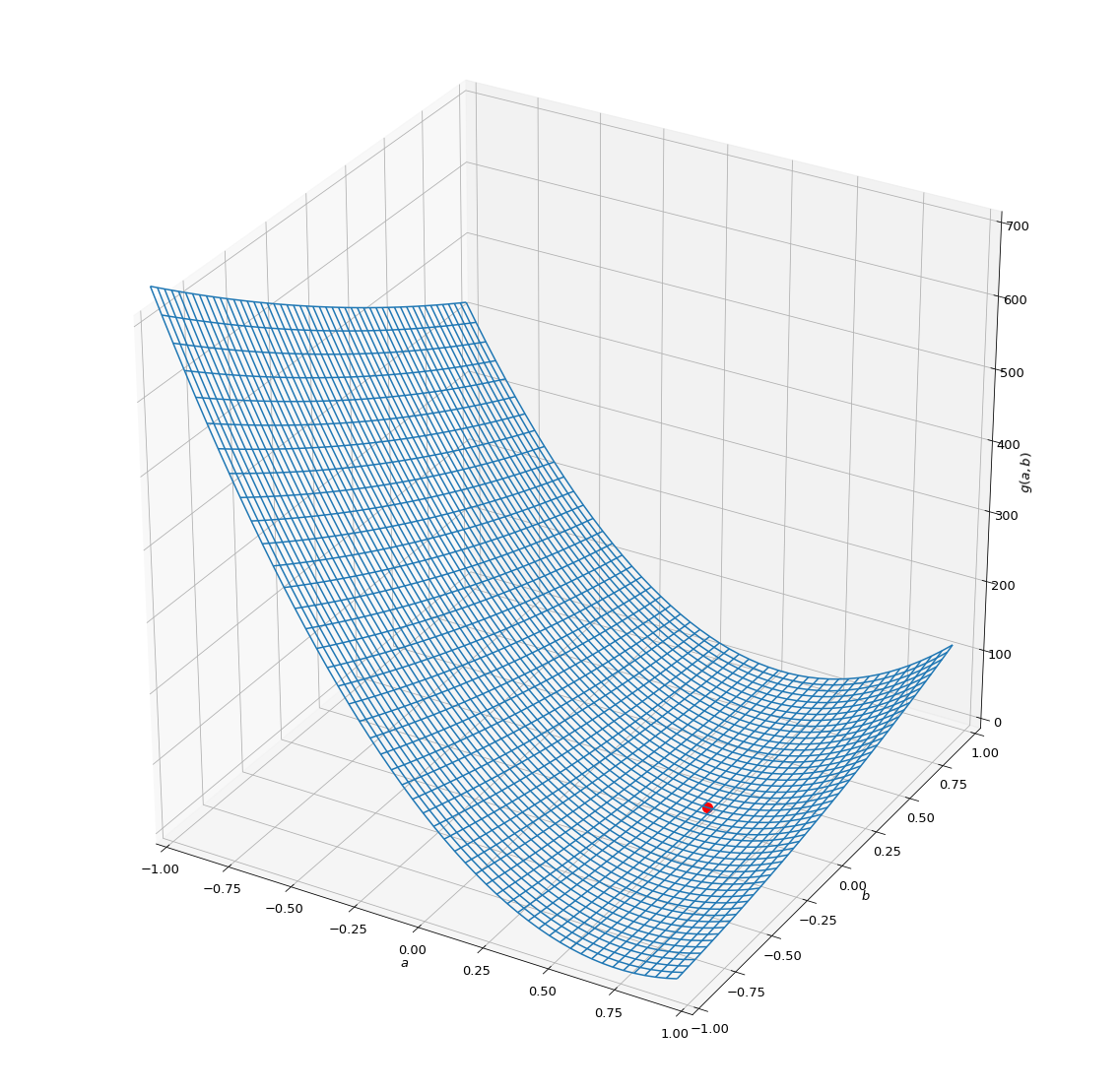
\[\begin{aligned} g(a, b) &= \color{red}y_1^2 - 2y_1(ax_1+b) + (ax_1+b)^2 \color{black} \\ &+ \color{green}y_2^2 - 2y_2(ax_2+b) + (ax_2+b)^2 \color{black}+ \dots \\ &+ \color{blue}y_n^2 - 2y_n(ax_n+b) + (ax_n+b)^2 \\\\ &= \color{red}y_1^2 - 2y_1ax_1 - 2y_1b + a^2x_1^2 + 2ax_1b + b^2 \color{black} \\ &+ \color{green}y_2^2 - 2y_2ax_2 - 2y_2b + a^2x_2^2 + 2ax_2b + b^2 \color{black}+ \dots \\ &+ \color{blue}y_n^2 - 2y_nax_n - 2y_nb + a^2x_n^2 + 2ax_nb + b^2 \\\\ &= (\color{red}y_1^2 + \color{green}y_2^2 + \color{black}\dots + \color{blue}y_n^2) \color{black} \\ &- 2a(\color{red}x_1y_1 + \color{green}x_2y_2 + \color{black}\dots + \color{blue}x_ny_n) \color{black} \\ &- 2b(\color{red}y_1 + \color{green}y_2 + \color{black} \dots + \color{blue}y_n) \color{black} \\ &+ a^2(\color{red}x_1^2 + \color{green}x_2^2 + \color{black} \dots + \color{blue}x_n^2) \color{black} \\ &+ 2ab(\color{red}x_1 + \color{green}x_2 + \color{black} \dots + \color{blue}x_n) \color{black} \\ &+ nb^2\\\\ &= n\times\overline{y^2} - 2an\times\overline{xy} - 2bn\times\overline{y} + a^2n\times\overline{x^2} + 2abn\times\overline{x} + nb^2 \end{aligned}\]Trong hình 2, điểm màu đỏ là “đáy” của mặt phẳng biểu diễn hàm \(g(a,b)\). Tức là tại điểm đó, \(g\) có giá trị cực tiểu và nhỏ nhất, nghĩa là đạo hàm tại điểm đó bằng 0:
\[dg(a,b) = \left[\begin{array}{cc}\frac{\partial g}{\partial a} & \frac{\partial g}{\partial b}\end{array}\right] = \left[\begin{array}{cc}0 & 0\end{array}\right]\]Như vậy,
\[\begin{cases} \frac{\partial g}{\partial a} = 0\\ \frac{\partial g}{\partial b} = 0 \end{cases} \Leftrightarrow \begin{cases} -2n\times\overline{xy} + 2an\times\overline{x^2} + 2bn\times\overline{x} = 0\\ -2n\times\overline{y} + 2an\times\overline{x} + 2bn = 0\\ \end{cases} \Leftrightarrow \begin{cases} a\overline{x^2} + b\overline{x} = \overline{xy}\\ a\overline{x} + b = \overline{y}\\ \end{cases}\]Giải hệ phương trình cuối cùng để tìm hai số \(a\) và \(b\), lúc này đường \(\hat{y} = f(x) = ax+b\) là best fit line cho tập điểm của chúng ta.
Có thể thấy rằng, trong các bước biến đổi cuối cùng, ta chia mỗi vế của hai phương trình cho \(2n\). Chính vì thế, nhiều tài liệu thường đặt hàm mục tiêu cần tối thiểu không phải là hàm \(g\), mà là hàm \(\frac{1}{2n}g\) để đơn giản hóa các bước tính toán.
Bài toán chiếc xe chuyển động thẳng đều ở trên chỉ có một biến độc lập đó là \(x\). Trong trường hợp biến \(y\) phụ thuộc vào \(k-1\) biến (\(k-1 > 0\)) \(x_2, x_2, \dots, x_k\).
Thay vì ghi \(\hat{y} = ax + b\) mình có thể ghi dạng nhân ma trận (đây là trường hợp \(k=2\)):
\[\hat{y} = \left[\begin{array}{cc}1 & x\end{array}\right]\times \left[\begin{array}{c}b \\ a\end{array}\right]\]Với cách viết này, mình có thể dễ dàng chuyển sang trường hợp tổng quát có \(k-1\) biến \(x\).
\[\hat{y} = \left[\begin{array}{ccc}x_1=1 & \dots & x_k\end{array}\right]\times \left[\begin{array}{c}a_1 \\ \dots\\ a_k\end{array}\right] = \left[\begin{array}{ccc}x_1=1 & \dots & x_k\end{array}\right]\times \textbf{a}\]Sở dĩ mình thêm một hằng số \(x_1 = 1\) vào vector biến \(\textbf{x}\) để khi nhân với vector hàng hệ số \(\textbf{a}\), thì phương trình tạo ra có hệ số tự do.
Giả sử bạn thực hiện \(n\) lần đo, lần thứ \(i\) thu được điểm \((x_{1,i}, x_{2,i}, \dots x_{k,i} = 1, y_i)\), thì hàm cần tối thiểu là:
\[g(\textbf{a}) = \left(y_1 - \left[\begin{array}{ccc}x_{1,1} & \dots & x_{k,1}\end{array}\right]\times\textbf{a}\right)^2 + \dots + \left(y_n - \left[\begin{array}{ccc}x_{1,n} & \dots & x_{k,n}\end{array}\right]\times\textbf{a}\right)^2\]Viết gọn,
\[g(\textbf{a}) = \sum_{i=1}^{n}\left(y_i - \left[\begin{array}{ccc}x_{1,i} & \dots & x_{k,i}\end{array}\right]\times\textbf{a}\right)^2\]Lưu ý, đừng nhầm lẫn giữa \(k\) (số phần tử của vector biến \(\textbf{x}\)) và \(n\) (số điểm trong bảng thống kê).
Bây giờ, chúng ta đạo hàm hàm \(g\), có được:
\[g'(\textbf{a}) = \sum_{i=1}^{n}\left(2\times\left[\begin{array}{c}x_{1,i} \\ \dots\\ x_{k,i}\end{array}\right]\left(\left[\begin{array}{ccc}x_{1,i} & \dots & x_{k,i}\end{array}\right]\times\textbf{a}-y_i\right)\right)\]Nếu đặt đạo hàm bằng 0, có phương trình sau:
\[\sum_{i=1}^{n}\left[\begin{array}{c}x_{1,i} \\ \dots\\ x_{k,i}\end{array}\right]\times \left(\left[\begin{array}{ccc}x_{1,i} & \dots & x_{k,i}\end{array}\right]\times\textbf{a}\right) \color{red}=\color{black} \sum_{i=1}^{n}\left[\begin{array}{c}x_{1,i} \\ \dots\\ x_{k,i}\end{array}\right]\times y_i\]Xét riêng, ta thấy:
\[\begin{aligned} &\sum_{i=1}^{n}\left[\begin{array}{c}x_{1,i} \\ \dots\\ x_{k,i}\end{array}\right]\times \left(\left[\begin{array}{ccc}x_{1,i} & \dots & x_{k,i}\end{array}\right]\times\textbf{a}\right)\\ =&\sum_{i=1}^{n}\left[\begin{array}{c}x_{1,i} \\ \dots\\ x_{k,i}\end{array}\right]\times\hat{y}_i\\ =&\ \color{red}\left[\begin{array}{ccc}x_{1,1} & \dots & x_{1,n}\\ \vdots & \ddots & \vdots\\ x_{k,1} & \dots & x_{k,n}\end{array}\right]\color{black}\times\color{blue}\left[\begin{array}{c}\hat{y}_1 \\ \dots \\ \hat{y}_n\end{array}\right] \color{black}\\ =&\ \color{red}\left[\begin{array}{ccc}x_{1,1} & \dots & x_{1,n}\\ \vdots & \ddots & \vdots\\ x_{k,1} & \dots & x_{k,n}\end{array}\right]\times\color{blue}\left[\begin{array}{ccc}x_{1,1} & \dots & x_{k,1}\\ \vdots & \ddots & \vdots\\ x_{1,n} & \dots & x_{k,n}\end{array}\right]\times\textbf{a}\color{black}\\ \triangleq&\ \color{red}\textbf{X}^T\color{blue}\textbf{X}\textbf{a} \end{aligned}\](kí hiệu \(\triangleq\) là “đặt bằng, gán bằng”)
và:
\[\begin{aligned} &\sum_{i=1}^{n}\left[\begin{array}{c}x_{1,i} \\ \dots\\ x_{k,i}\end{array}\right]\times y_i\\ =&\color{red}\left[\begin{array}{ccc}x_{1,1} & \dots & x_{1,n}\\ \vdots & \ddots & \vdots\\ x_{k,1} & \dots & x_{k,n}\end{array}\right]\color{black}\times\color{blue}\left[\begin{array}{c}y_1 \\ \dots \\ y_n\end{array}\right] \\ \triangleq&\ \color{red}\textbf{X}^T\color{black}\color{blue}\textbf{y} \end{aligned}\]Quay lại phương trình vừa nãy, ta có:
\[\textbf{X}^T\textbf{Xa} = \textbf{X}^T\textbf{y}\]Nếu \(\textbf{X}^T\textbf{X}\) tồn tại ma trận nghịch đảo (inverse matrix) thì:
\[\textbf{a} = \left(\textbf{X}^T\textbf{X}\right)^{-1}\textbf{X}^T\textbf{y}\]nếu không thì lấy ma trận giả nghịch đảo (pseudo inverse matrix):
\[\textbf{a} = \left(\textbf{X}^T\textbf{X}\right)^{\dagger}\textbf{X}^T\textbf{y}\]Như vậy chúng ta đã tìm ra được nghiệm bài toán.
Xem Jupyter Notebook
Special thanks to my friends, Can Tran Thanh Trung, Vu Le The Anh, for their precious advice.