My visit to Dak Nong

Hôm nay mình muốn bình về bài toán VAIMIN đăng trên CodeChef trong kỳ thi April Challenge 2018. Đây là một bài toán phức tạp song có rất nhiều kỹ thuật và kiến thức hữu ích rút ra được từ nó

Tóm tắt

Một thủ tướng có thể làm điều tốt hoặc điều xấu. Mức độ uy tín của ông tăng lên 1 khi ông làm điều tốt và giảm đi 1 khi ông làm điều xấu. Ban đầu, mức độ uy tín là bằng 0. Ông ta lên kế hoạch làm đủ \(p\) điều tốt và \(q\) điều xấu. Tuy nhiên, trước khi làm một điều xấu, uy tín của ông ta phải lớn hơn \(c\), nếu không ông sẽ bị phát hiện và buộc từ chức!

Có một ông thanh tra chuyên đi bắt các vụ tham nhũng. Vị thanh tra từng bắt \(M\) bộ trưởng tham nhũng, khi bộ trưởng \(i\) bị bắt, hắn đã từng làm \(g_i\) điều tốt và \(b_i\) điều xấu. Không muốn đi vào con đường cũ, ngài thủ tướng sẽ tránh làm \(g_i\) điều tốt và \(b_i\) điều xấu trong suốt nhiệm kì của mình, bởi không ngài sẽ bị bắt bởi vị thanh tra kia.

Hãy đếm số chiến thuật thực hiện điều tốt xấu trong nhiệm kì của thủ tướng sao cho thỏa mãn các điều kiện trên.

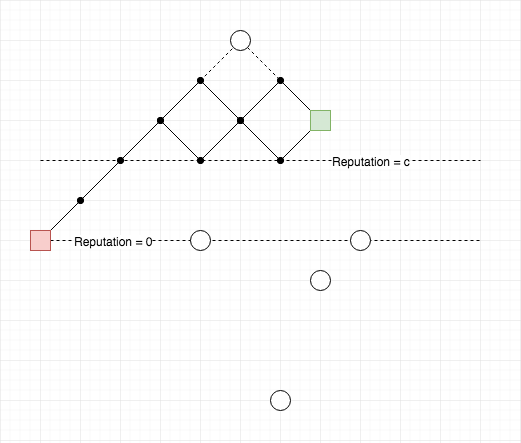
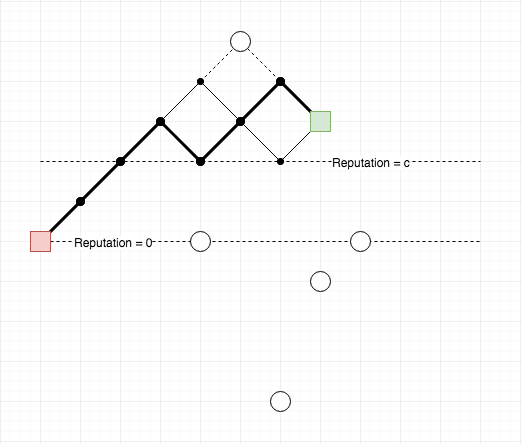
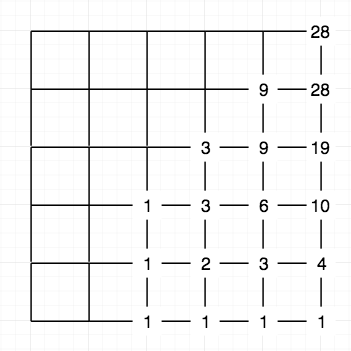
Với bộ test mẫu của đề bài: \(p = 5\), \(q = 2\), \(c = 2\), \(M = 5\). Ta có hình minh họa ở hình 1:

Minh họa test mẫu đề bài

Các hình tròn trắng khoanh vùng điểm “cấm” (điểm mà các bộ trưởng bị bắt hối lộ). Ban đầu thủ tướng đứng ở hình vuông đỏ, rồi tìm cách đi đến hình vuông xanh lá. Mỗi bước đi tuân thủ những điều kiện sau:

  • Bắt buộc phải đi lên (hướng đông bắc) hoặc đi xuống (hướng đông nam);
  • Mọi bước đi xuống đều không được rơi xuống bên dưới đường Reputation = \(c\).
  • Không được đi vào những điểm cấm.

Hỏi có bao nhiêu cách đi?

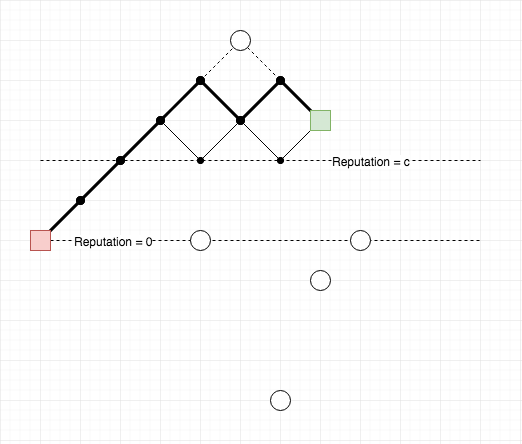
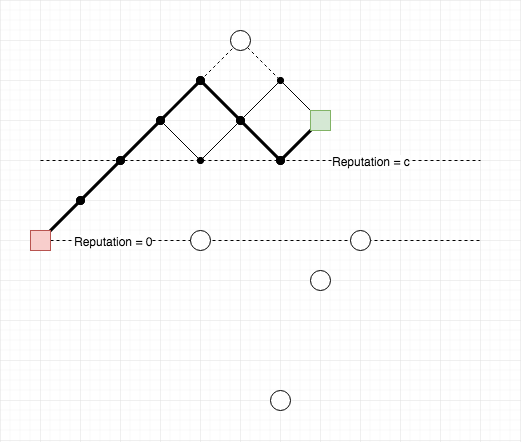
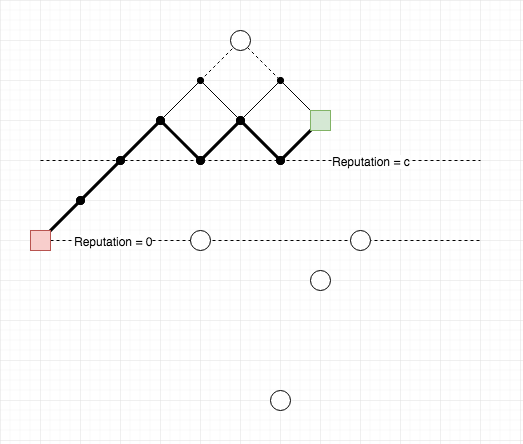
Trong ví dụ trên, có tổng cộng 4 cách đi:

Cách 1

Cách 2

Cách 3

Cách 4

Khởi động

Trước khi bước vào bài toán trên, ta hãy bắt đầu từ một bài toán đơn giản trước. Cho một lưới ô vuông với tọa độ góc trái dưới là \((0,0)\) và góc trái trên là \((m,n)\). Có bao nhiêu cách đi từ góc trái dưới đến góc trái trên của bảng (với điều kiện chỉ có thể đi qua phải hoặc đi lên)?

Phân tích đơn giản như sau: Nếu chúng ta gọi bước đi sang phải là R và bước đi lên là U, thì hành trình từ góc trái dưới đến góc trái trên là một chuỗi nhị phân U-R có độ dài \(m+n\). Mặt khác, chuỗi này phải có đúng \(m\) ký tự R (và hệ quả tất yếu là có \(n\) ký tự U), nên số hành trình tìm được là:

\[\binom{m+n}{m} = \binom{m+n}{n} = \frac{(m+n)!}{m!n!}\]

(tương đương với bài toán chọn ra \(m\) vị trí trong số \(m+n\) vị trí trong chuỗi để đặt ký tự R vào đó).

Lưới ô vuông 6 x 5.
Có 462 cách để đi từ (0, 0) đến (6, 5).

Nếu gọi số cách di chuyển từ điểm \((0,0)\) đến điểm \((i,j)\) là \(f(i,j)\), công thức đệ quy sẽ là:

\[f(i,j) = \begin{cases} 0, & \mathrm{if\ point}\ (i,j)\ \mathrm{is\ out\ of\ the\ grid}\\ 1, & \mathrm{if}\ i = 0\ \mathrm{and}\ j = 0\\ f(i-1, j) + f(i, j-1), & \mathrm{otherwise} \end{cases}\]

Hay quen thuộc hơn:

\[f(i,j) = \binom{i+j}{i} = \binom{i+j-1}{i-1} + \binom{i+j-1}{i} = f(i-1, j) + f(i, j-1)\]

Công thức trên rất dễ hiểu: vì để đến được điểm \((i,j)\), ta phải đến điểm \((i-1,j)\) hoặc \((i,j-1)\) trước, nên số cách tại điểm \((i,j)\) bằng tổng số cách tại hai điểm trước.

Lưới có điểm bị chặn

Giả sử vì một lý do nào đó, một vài điểm trên lưới bị chặn, chúng ta không được bước vào điểm đó. Lúc này, công thức tổ hợp tỏ ra rất khó để chỉnh sửa, tuy nhiên công thức đệ quy chỉ cần thêm một vài điều kiện neo nhỏ là có thể đưa ra kết quả đúng.

\[f(i,j) = \begin{cases} 0, & \mathrm{if\ point}\ (i,j)\ \mathrm{is\ out\ of\ the\ grid\ or\ prohibited}\\ 1, & \mathrm{if}\ i = 0\ \mathrm{or}\ j = 0\\ f(i-1, j) + f(i, j-1), & \mathrm{otherwise} \end{cases}\]

Mặt khác, công thức đệ quy tỏ ra thiếu hiệu quả nếu lưới có kích thước lớn, chúng ta cần quay lại công thức tổ hợp để giảm độ phức tạp thời gian.

Một điểm bị chặn

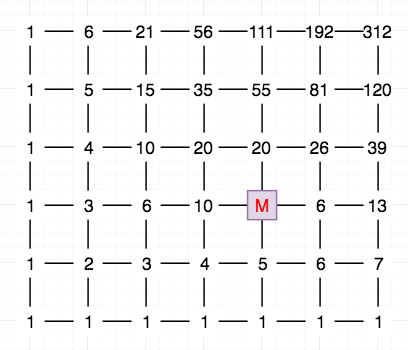
Bắt đầu với trường hợp trên lưới có một điểm bị chặn \(M(a, b)\).

Lưới với một điểm bị chặn.
Có 312 cách để đi từ (0, 0) đến (6, 5) mà không đi qua M.

Gọi \(g(i,j)\) là số cách đi từ \((0, 0)\) đến \((i,j)\) mà không đi qua điểm bị chặn. Ta cần quan tâm đến \(\alpha\) bằng số cách đi từ \((0,0)\) đến ô cấm \((a,b)\) rồi tiếp tục từ đó đến \((i,j)\), để trừ bớt lượng này khỏi số cách đi thông thường khi chưa có điểm cấm. Có hai thao tác để đi đến \((i,j)\) thông qua \((a,b)\):

  • Đi từ \((0, 0)\) đến \((a, b)\). Có \(f(a,b)\) cách đi như thế.
  • Đi từ \((a, b)\) đến \((i, j)\). Ta xem đây là hai góc của một hình chữ nhật mới, suy ra có \(f(i - a, j - b)\) cách đi như thế.

Sử dụng công thức nhân, \(\alpha = f(a, b) \times f(i-a, j-b)\) cách đi đến \((i,j)\) thông qua \((a,b)\).

Lưu ý rằng, do chúng ta chỉ xét hướng đi lên và sang phải, nên trong trường hợp \(i<a\) hoặc \(j<b\), chúng ta không bao giờ gặp ô cấm, nên cứ đi như thông thường.

Vậy:

\[g(i,j) = \begin{cases} f(i,j) - f(a,b) \times f(i-a, j-b) & \mathrm{if}\ i \geq a\ \mathrm{and}\ j\geq b\\ f(i,j) & \mathrm{otherwise} \end{cases}\]

Thay các hàm \(f\) này bằng công thức tổ hợp sẽ cho ra công thức tổ hợp tương ứng cho hàm \(g\).

Nhiều điểm bị chặn

Câu hỏi đặt ra là, nếu trên lưới có nhiều điểm bị chặn thì làm sao? Gọi \(S = \{M_1, M_2, \dots, M_q\}\) là tập các điểm bị chặn trên lưới. Về phương diện toán học, câu trả lời nằm ở nguyên lý thêm bớt (aka inclusion-exclusion principle). Nếu gọi \(h(T)\) là số đường đi đi qua tất cả các điểm trong \(T\), thì số đường đi tránh các điểm trong \(S\) bằng:

\[\sum_{T\subset\ S} (-1)^{|T|}h(T)\]

với \(h(\varnothing ) = \binom{m+n}{n}\)

Tuy nhiên, mình chưa bao giờ là một fan của nguyên lý này bởi độ phức tạp thuật toán để triển khai nó thường là quá cao. Chúng ta sẽ tập trung vào cách giải khả thi hơn, dù kém khái quát hơn.

Gọi \(g_k(i,j)\) là số cách đi đến điểm \((i,j)\) nếu \(M_1, M_2, \dots, M_k\) bị chặn. Ta có ý tưởng về công thức truy hồi như sau:

  • \(g_0(i,j) = f_0(i,j),\ \forall i,j\)  
  • \(g_k(i,j) = \begin{cases}g_{k-1}(i,j) - g_{k-1}(a_k, b_k)\times g_{k-1}(i-a_k, j-b_k) & \mathrm{if}\ i \geq a_k\ \mathrm{and}\ j\geq b_k\\ g_{k-1}(i,j) & \mathrm{otherwise}\end{cases}\)  

Tuy nhiên, đây chỉ mới là “ý tưởng”, chưa thực sự chính xác và hoàn thiện. Khiếm khuyết của nó ở chỗ, \(g_{k-1}(i-a_k, j-b_k)\) thực tế nên là cho “số cách đi từ \((a_k,b_k)\) đến \((i,j)\) sau khi \(M_1, M_2, \dots, M_{k-1}\) bị chặn”. Còn ý nghĩa của \(g_{k-1}(i-a_k, j-b_k)\) lại là “số cách đi từ \((0,0)\) đến \((i-a_k, j-b_k)\) sau khi \(M_1, M_2, \dots, M_{k-1}\) bị chặn”. Hai điều này không hề tương đương với nhau. Khi lưới không bị chặn bởi điểm nào, chúng có tương đương vì có cùng hình dạng là lưới chữ nhật kích thước \((i-a_k)\times(j-b_k)\). Khi có điểm chặn xuất hiện, hình dạng của hai lưới chữ nhật từ \((0,0)\) đến \((i-a_k, j-b_k)\) và từ \((a_k,b_k)\) đến \((i,j)\) có thể không còn như nhau nữa.

Hãy để ý rằng có một số trường hợp mà đi từ một điểm này đến một điểm kia không bao giờ gặp điểm chặn. Đó là khi điểm chặn không nằm trong lưới chữ nhật giới hạn bởi hai điểm này. Trong những trường hợp như vậy, việc tính toán số đường đi từ \((a_k,b_k)\) đến \((i,j)\) có thể được rút gọn xuống hàm \(f(i-a_k,j-b_k)\).

Nếu ta sắp xếp các điểm chặn theo một thứ tự sao cho với \(x\) bất kì, không tồn tại bất cứ điểm nào trong các điểm \(M_1, M_2, \dots, M_{x-1}\) nằm trong lưới chữ nhật có góc trái dưới \(M_x\) và góc trái trên \((i,j)\) nào hợp lệ, thì việc tính toán “số cách đi từ \((a_k,b_k)\) đến \((i,j)\) sau khi \(M_1, M_2, \dots, M_{k-1}\) bị chặn” chỉ đơn thuần là \(f(i-a_k, j-b_k)\) (thậm chí không dùng đến hàm \(g\)!!).

Lưu ý mình dùng chữ “hợp lệ” – vì bạn có thể tính \(g_k(i,j)\) tại nhiều điểm \((i,j)\) khác nhau, nhưng dù ở điểm nào, nếu một \(M_x\) nào đó tạo với \((i,j)\) một hình chữ nhật với \(M_x\) là góc trái dưới, \((i,j)\) là góc trái trên, thì mọi \(M_1, M_2,\dots, M_{x-1}\) đều nằm ngoài hình chữ nhật này; còn nếu chúng không tạo thành hình chữ nhật thì lại càng đơn giản vì khi đấy \(g_k(i,j) = g_{k-1}(i,j)\)

Cụ thể hơn, cách sắp xếp đó là xếp các điểm tăng dần theo hoành độ. Các điểm có hoành độ bằng nhau được xếp tăng dần theo tung độ.

Như vậy, để tính \(g_q(m,n)\), chúng ta có nhất thiết phải tính \(g_k(i,j)\) cho mọi giá trị \(i,j,k\)? Không. Tính toán như thế cực kỳ tốn kém với độ phức tạp \(O(m\times n\times k)\). Một cách đi gọn hơn là chỉ cần tính \(g_k\) tại các điểm cấm, giảm độ phức tạp xuống chỉ còn \(O(k^2)\).

Hình thang Catalan

Lưới có hình tam giác

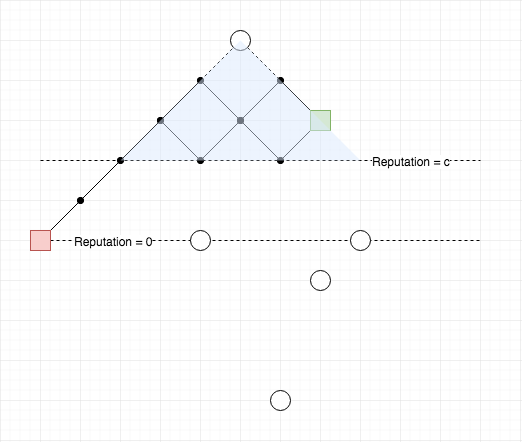
Trở lại bài toán gốc của chúng ta. Chúng ta nhận ra \(c+1\) bước đầu tiên phải là hướng đi lên, vì hướng đi xuống không được rớt xuống dưới đường Reputation = \(c\). Tất cả phép màu chỉ diễn ra từ đường Reputation = \(c\) trở lên. Đó không phải hình dạng của một lưới hình vuông, mà lại là một tam giác.

Có một khái niệm trong toán học là số Catalan. Tức số cách di chuyển từ điểm \((0,0)\) đến điểm \((\nu,\nu)\) nhưng chỉ được đi ở một phía của lưới. Nó được tính bằng công thức:

\[C_{\nu} = \frac{1}{\nu+1}\binom{2\nu}{\nu}\]

Tam giác Catalan

Tổng quát hơn, số cách đi từ \((0,0)\) đến \((\nu,\kappa)\) mà không lấn qua nửa kia của tam giác sẽ bằng:

\[C(\nu,\kappa) = \begin{cases}1 & \mathrm{if}\ \kappa = 0\\ \binom{\nu+\kappa}{\kappa} - \binom{\nu+\kappa}{\kappa-1} & \mathrm{otherwise}\end{cases}\]

Song, chúng ta cần tiếp tục tổng quát hóa công thức này nữa. Vì trong quá trình tìm \(g_q(m,n)\), chúng ta thường xuyên bắt gặp tình huống tính số cách đi từ \((a_k, b_k)\) đến \((i, j)\) – vốn là những tọa độ có thể ở bất kì đâu. Và lưu ý, do các công thức chúng ta đã xây dựng phụ thuộc nhiều vào điểm kết thúc, việc thay đổi điểm bắt đầu sẽ thay đổi công thức rất lớn. Quan sát hình tam giác Catalan, bắt đầu từ góc \((0,0)\), nhưng đến bất cứ đâu trên tam giác cũng dùng một công thức vì cách mà chúng ta xây dựng công thức. Nếu chẳng may ta phải đi từ, ví dụ như điểm (2,0), cả bảng số sẽ thay đổi.

Hình thang Catalan cấp 3

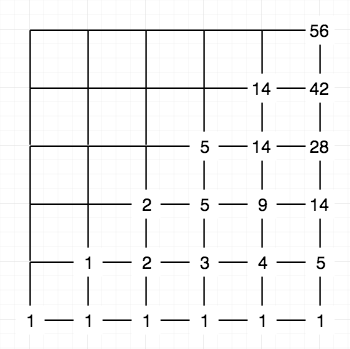
Như vậy chúng ta phải thêm một (hoặc một vài) tham số mới thay vì giữ nguyên hàm \(f\) như ở lưới hình vuông ở trên. Ta quan tâm đến \(\mu\) là số điểm trên đáy nhỏ hình thang (thực tế đáy lớn hình thang này có thể được mở ra đến vô tận).

Hình thang Catalan là khái niệm tổng quát hơn của tam giác Catalan. Cụ thể, xuất phát từ \((\mu-1, 0)\). Có bao nhiêu đường đi đơn điệu để đi đến điểm \((\nu,\kappa)\) sao cho không được vượt qua đường chéo chính? Câu trả lời là:

\[C_{\mu}(\nu, \kappa) = \begin{cases} \binom{\nu+\kappa}{\kappa} & 0\leq \kappa < \mu\\ \binom{\nu+\kappa}{\kappa} - \binom{\nu+\kappa}{\kappa-\mu} & \mu \leq \kappa \leq \nu+\mu-1\\ 0 & k > \nu+\mu-1 \end{cases}\]

Thêm điểm chặn

Khi thêm các điểm chặn lên lưới tam giác, logic tính toán \(g_q(m,n)\) vẫn đúng vì cách lập luận của chúng ta độc lập với không gian được phép di chuyển (hình dạng lưới). Dù bạn có đổi sang hình… tròn thay vì hình tam giác thì những logic đó vẫn đúng. Ta có tổng hợp dưới đây:

  • Công thức hình thang Catalan tính số đường đi đơn điệu từ một điểm này đến một điểm kia trên một lưới tam giác (không có vật cản).

  • \(g_k(i,j) = \begin{cases}g_{k-1}(i,j) - g_{k-1}(a_k, b_k)\times F(a_k, b_k, i, j) & \mathrm{if}\ i \geq a_k\ \mathrm{and}\ j\geq b_k\\ g_{k-1}(i,j) & \mathrm{otherwise}\end{cases}\)  

  • \[g_0(i,j) = F(0,0,i,j)\]
  • \(F(u_1, v_1, u_2, v_2)\) là số cách đi từ điểm \((u_1,v_1)\) đến \((u_2,v_2)\) tính theo công thức hình thang Catalan:
\[F(u_1, v_1, u_2, v_2) = C_{u_1 - v_1 + 1}(v_2 - v_1, u_2 - u_1)\]

với điều kiện tập \(S\) các điểm chặn được sắp xếp tăng dần theo tọa độ và hàm \(F\) được tính với giả sử không có vật cản trên lưới tam giác.

Biến đổi tọa độ

Ta thấy rằng lưới tam giác trong bài toán gốc là một tam giác Catalan hoàn hảo, chỉ khác ở góc nhìn. Bằng một số phép xoay và dịch chuyển tọa độ sẽ ra đưa bài toán đó về tam giác Catalan.

Cảm nhận

Thực sự viết những bài này rất tốn sức. Giá mà có ai đó trả tiền cho mình :v . Số Catalan và những vấn đề liên quan có rất nhiều bài toán thú vị xoay quanh. Mời các bạn đọc thêm tại A000108 OEIS.

Nguồn: Tớ đã giải bài này trên CodeChef. Proof (not recommended as reference source).